✅ RB 트리 삽입/삭제 Case 정리
Insert-fixup
- 부모도 RED, 삼촌도 RED
→ 부모와 삼촌을 BLACK으로 바꾸고 할아버지를 RED로 바꾼 후 할아버지에서 다시 확인 - 삽입된 노드가 부모의 오른쪽 자녀, 부모가 RED이고 할아버지의 왼쪽 자녀, 삼촌은 BLACK
→ 부모를 기준으로 왼쪽으로 회전한 후 Case 3 방식으로 해결 - 삽입된 노드가 부모의 왼쪽 자녀, 부모가 RED이고 할아버지의 왼쪽 자녀, 삼촌은 BLACK
→ 부모와 할아버지의 색을 바꾼 후 할아버지 기준으로 오른쪽으로 회전
Delete
- 삭제하려는 노드의 자녀가 없거나 하나라면, 삭제되는 색 = 삭제되는 노드의 색
- 삭제 노드의 왼쪽 자식이 NIL일 때
→ 삭제 노드를 오른쪽 자식으로 대체함 - 삭제 노드의 오른쪽 자식이 NIL일 때
→ 삭제 노드를 왼쪽 자식으로 대체함
- 삭제 노드의 왼쪽 자식이 NIL일 때
- 삭제하려는 노드의 자녀가 둘이라면, 삭제되는 색 = 삭제되는 노드의 후임자의 색
- 삭제 노드의 후임자가 손자 이하일 때
→ 삭제 노드를 후임자로, 후임자를 그 오른쪽 자식으로 대체함 - 삭제 노드의 오른쪽 자식이 후임자일 때
→ 삭제 노드를 오른쪽 자식으로, 오른쪽 자식을 오른쪽 손자로 대체함
- 삭제 노드의 후임자가 손자 이하일 때
Delete-fixup
- DOUBLY BLACK의 오른쪽 형제가 RED일 때
→ 부모와 형제의 색을 바꾸고 부모를 기준으로 왼쪽으로 회전한 뒤, DOUBLY BLACK을 기준으로 Case 2, 3, 4 중 하나로 해결 - DOUBLY BLACK의 형제가 BLACK and 그 형제의 두 자녀가 모두 BLACK일 때
→ DOUBLY BLACK과 그 형제의 BLACK을 모두 모아서 부모에게 전달해서 부모가 EXTRA BLACK을 해결하도록 한다 - DOUBLY BLACK의 오른쪽 형제가 BLACK and 그 형제의 왼쪽 자녀가 RED and 오른쪽 자녀가 BLACK일 때
→ 형제와 형제의 왼쪽 자식 색을 바꾸고, 형제를 기준으로 오른쪽으로 회전하면 형제는 RED인 오른쪽 자식을 가진 BLACK이 되고, 이후에는 Case 4를 적용하여 해결 - DOUBLY BLACK의 오른쪽 형제가 BLACK and 그 형제의 오른쪽 자녀가 RED일 때
→ 오른쪽 형제는 부모의 색으로, 오른쪽 형제의 오른쪽 자녀는 BLACK으로, 부모는 BLACK으로 바꾼 후에 부모를 기준으로 왼쪽으로 회전하면 해결
int arr[] = {10, 5, 8, 34, 67, 23, 156, 24, 2, 12, 24, 36, 990, 25};위와 같이 선언된 배열 arr의 요소들이 순서대로 RB트리에 삽입/삭제되는 모습을 보자.
1. 삽입
(1) 10 삽입

- 10은 루트이므로 BLACK으로 바꾼다.
(2) 5 삽입

(3) 8 삽입

- [Case 2] 5를 기준으로 left-rotate한다.
- [Case 3] 8과 10의 색을 바꾼 후, 10을 기준으로 right-rotate한다.
(4) 34 삽입

- [Case 1] 5와 10을 BLACK으로 바꾸고 8을 RED로 바꾼 후, 8에서 다시 확인한다.
- 8은 루트이므로 BLACK으로 바꾸고 종료한다.
(5) 67 삽입

- [Case 3] 34와 10의 색을 바꾼 후, 10을 기준으로 left-rotate한다.
(6) 23 삽입

- [Case 1] 10과 67을 BLACK으로 바꾸고 34를 RED로 바꾼 후, 34에서 다시 확인한다.
- 34의 부모 8은 BLACK이므로 종료한다.
(7) 156 삽입
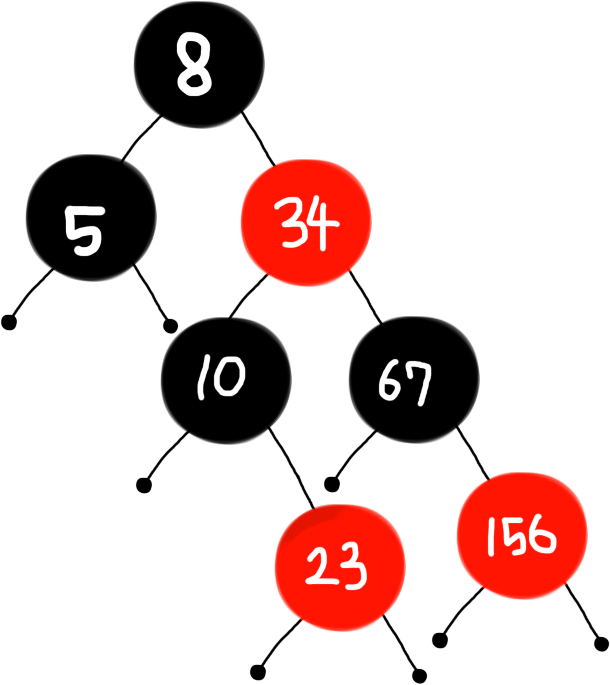
(8) 24 삽입
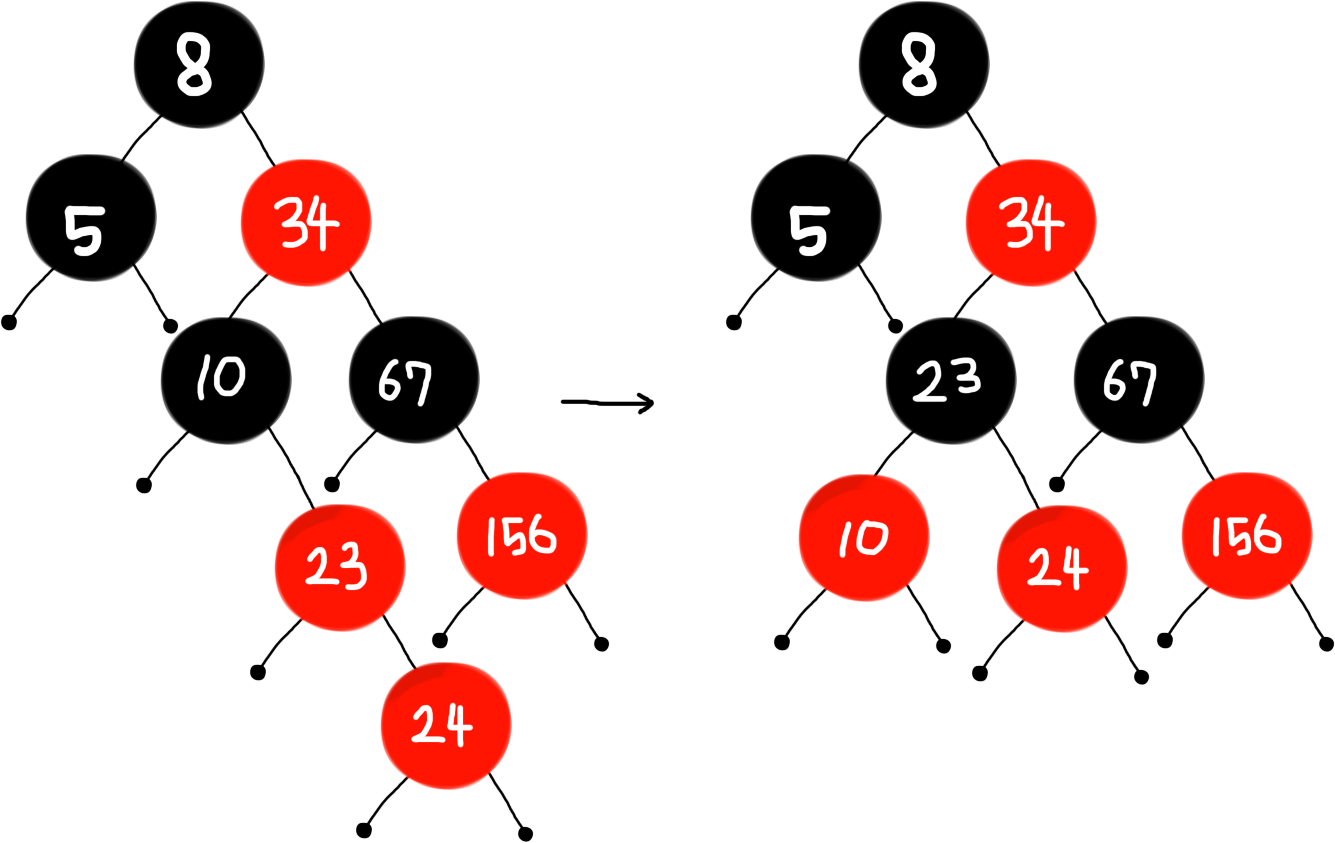
- [Case 3] 23과 10의 색을 바꾼 후, 10을 기준으로 left-rotate한다.
(9) 2 삽입

(10) 12 삽입
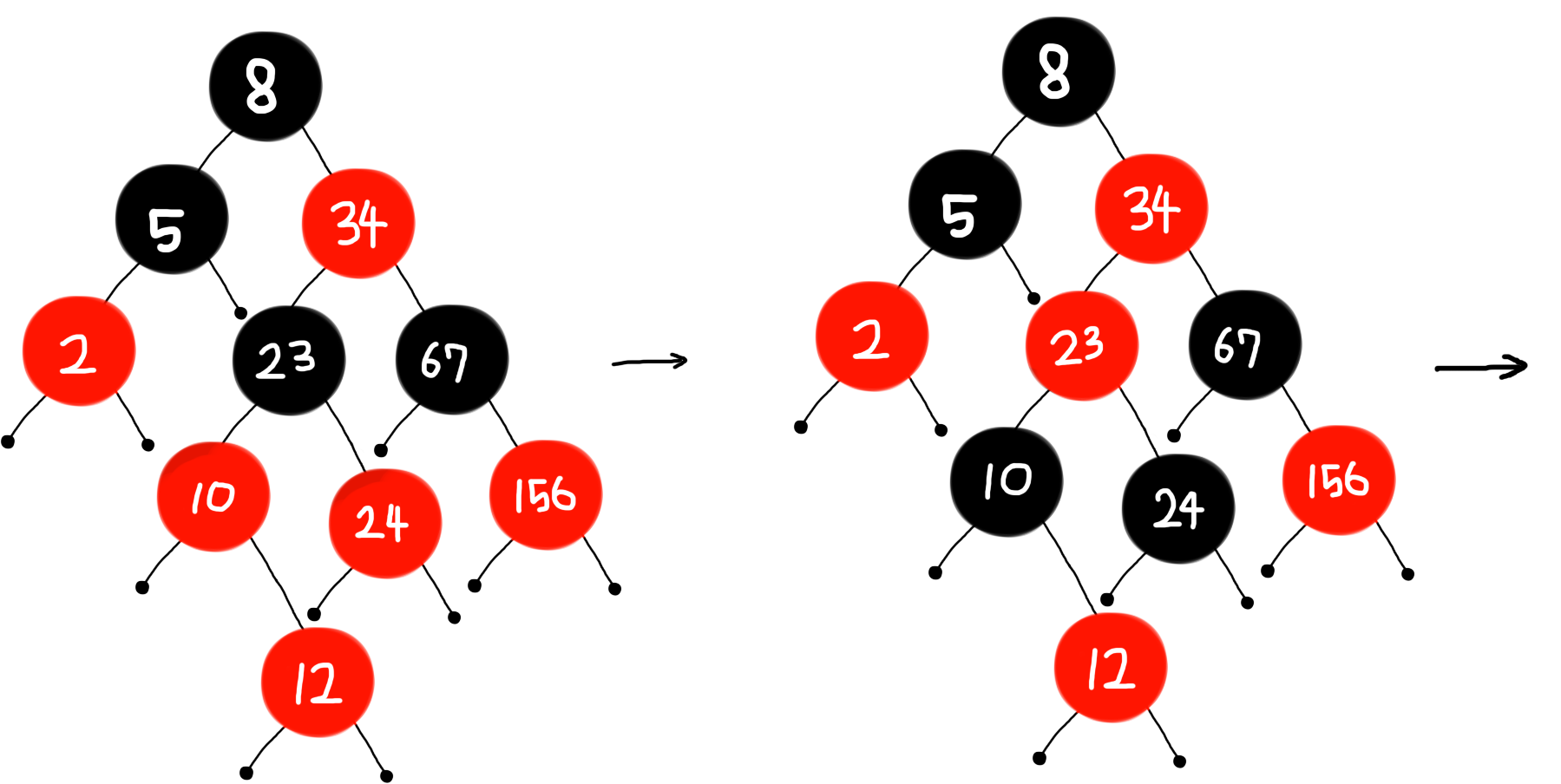

- [Case 1] 10과 24를 BLACK으로, 23을 RED로 바꾼 후, 23에서 다시 확인한다.
- [Case 2] 23을 기준으로 right-rotate한다.
- [Case 3] 23과 8의 색을 바꾼 후, 8을 기준으로 left-rotate한다.
(11) 24 삽입
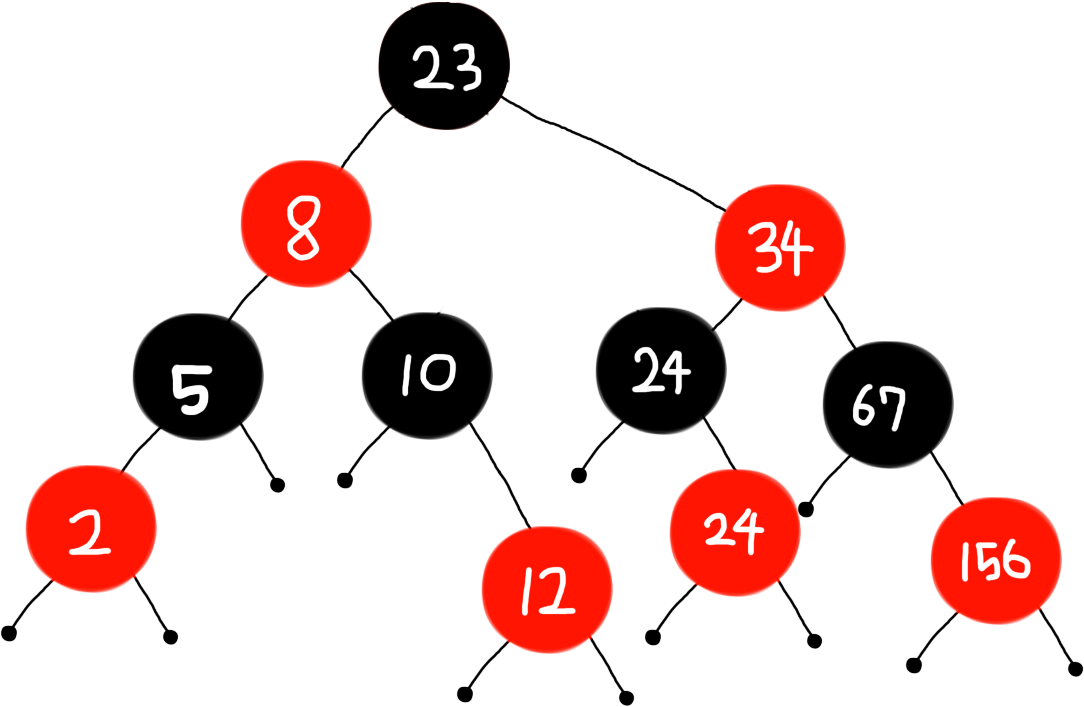
(12) 36 삽입

(13) 990 삽입

- [Case 1] 36과 156을 BLACK으로, 67을 RED로 바꾼 후, 67에서 다시 확인한다.
- [Case 1] 8과 34를 BLACK으로, 23을 RED로 바꾼 후, 23에서 다시 확인한다.
- 23은 루트이므로 BLACK으로 바꾸고 종료한다.
(14) 25 삽입

- [Case 3] 24와 24의 색을 바꾼 후, 24를 기준으로 왼쪽으로 회전한다.
삽입이 모두 완료된 후의 RB 트리는 다음과 같다.
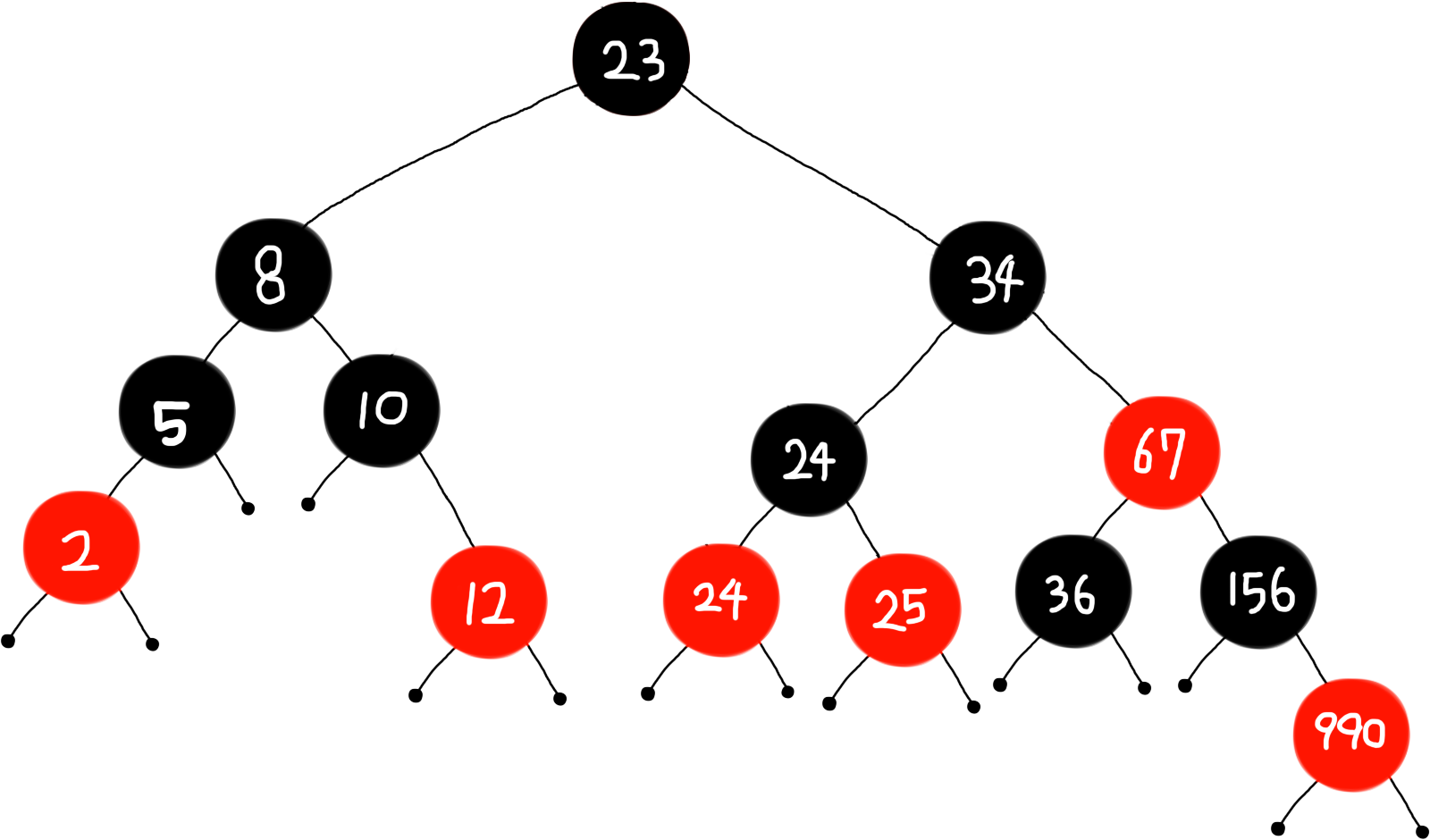
2. 삭제
(1) 10 삭제

- 10은 자식이 1개이므로 삭제되는 색은 BLACK
- 12가 10을 대체하여 RED-AND-BLACK이 됨 → BLACK으로 바뀌고 종료
(2) 5 삭제

- 5는 자식이 1개이므로 삭제되는 색은 BLACK
- 2가 5을 대체하여 RED-AND-BLACK이 됨 → BLACK으로 바뀌고 종료
(3) 8 제거


- 8은 자식이 2개이므로 삭제되는 색은 후임자 12의 BLACK
- 8을 12로, 12를 NIL로 대체함
- [Case 2] NIL을 BLACK으로, 2를 RED로 바꾸고 12에 EXTRA BLACK을 전달한다.
- [Case 4] 34는 BLACK으로, 67은 BLACK으로, 23은 BLACK으로 바꾼 후, 23를 기준으로 left-rotate한다.
(4) 34 제거

- 34는 자식이 2개이므로 삭제되는 색은 후임자 36의 BLACK
- 34는 36으로, 36은 NIL로 대체
- [Case 4] 156은 BLACK으로, 990은 BLACK으로, 67은 BLACK으로 바꾼 후, 67을 기준으로 left-rotate한다.
(5) 67 제거

- 67은 자녀가 없으므로 삭제되는 색은 BLACK
- [Case 2] NIL을 BLACK으로, 990을 RED로 바꾼 후 156을 DOUBLY BLACK으로 바꾼다.
- [Case 2] 156을 BLACK으로, 23을 RED로 바꾼 후 36을 DOUBLY BLACK으로 바꾼다.
- 36은 루트이므로 BLACK으로 바꾸고 종료한다.
(6) 23 제거

- 23은 자식이 2개이므로 삭제되는 색은 후임자 24의 RED
- 23은 24로, 24는 NIL로 대체하고 종료한다.
(7) 156 제거

- 156은 자식이 1개이므로 삭제되는 색은 BLACK
- 156은 990으로 대체하고, RED-AND-BLACK을 BLACK으로 바꾸고 종료한다.
(8) 24 제거

- 24는 자식이 2개이므로 삭제되는 색은 후임자 24의 BLACK
- 24는 24로 대체되고, 24는 25로 대체된다.
- 25는 RED-AND-BLACK이므로 BLACK으로 바꾸고 종료한다.
(9) 2 제거

- 2는 자식이 없으므로 삭제되는 색은 RED
- 2를 지우면 끝
(10) 12 제거
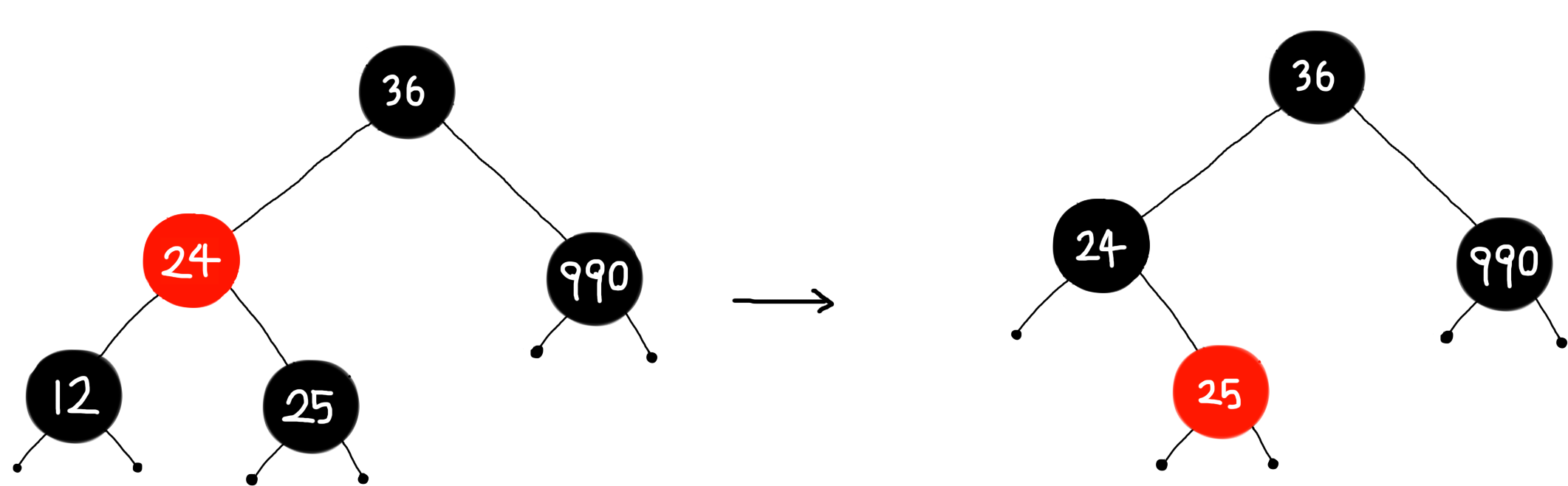
- 12는 자식이 없으므로 삭제되는 색은 BLACK
- [Case 2] NIL을 BLACK으로, 25를 RED로 바꾼 후, 24에 EXTRA BLACK을 추가한다.
- 24는 RED-AND-BLACK이므로 BLACK으로 바꾸고 종료한다.
(11) 24 제거
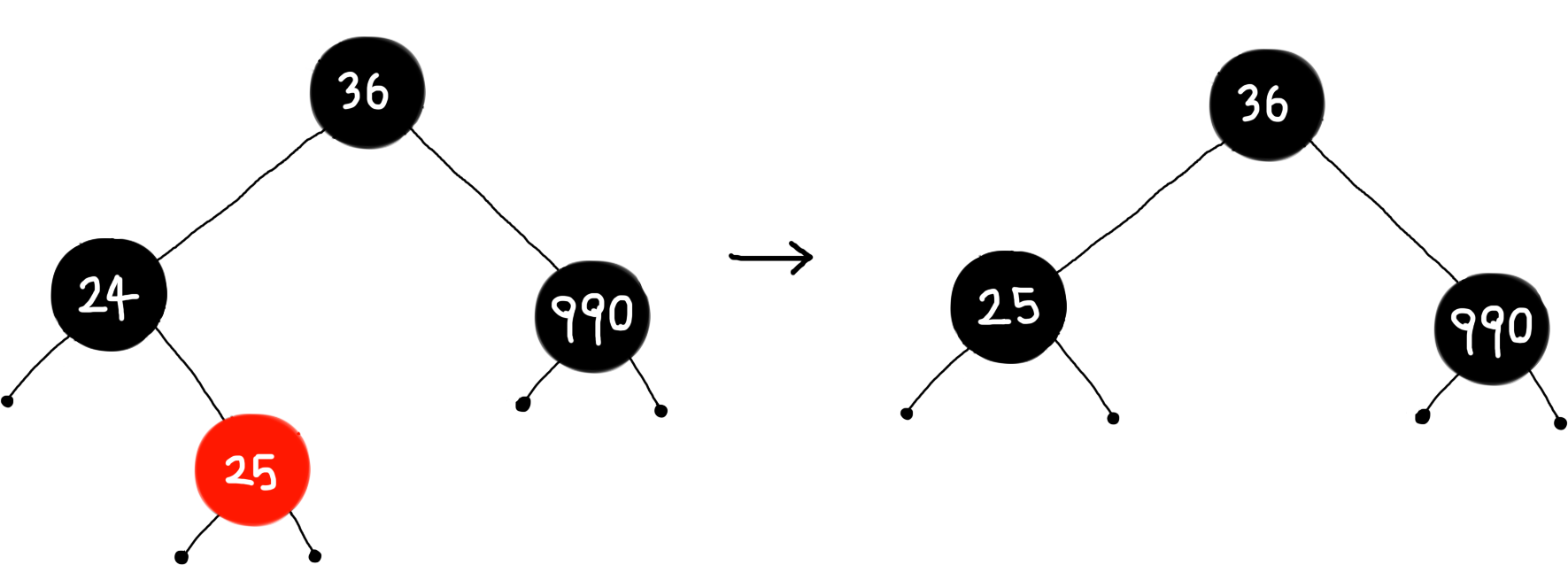
- 24는 자식이 1개이므로 삭제되는 색은 BLACK
- 24를 25로 대체, 25를 NIL로 대체한다.
- 25는 RED-AND-BLACK이므로 BLACK으로 바꾸고 종료한다.
이후로는 하나씩 제거되어 최종적으로는 RB 트리가 비게 된다.
'Krafton Jungle > 3. TIL' 카테고리의 다른 글
| [WEEK06] AVL 트리 vs RB 트리 성능 분석 (2) | 2025.04.23 |
|---|---|
| [WEEK06] RB 트리 Case 정리 (0) | 2025.04.22 |
| [WEEK06] RB트리의 삽입/삭제에 대해 우리집 강아지 문식이도 알기 쉽게 설명해줘 (0) | 2025.04.19 |
| [WEEK06] 레드-블랙 트리에 대해 우리집 강아지 문식이도 알기 쉽게 설명해줘 (0) | 2025.04.15 |
| [WEEK05] 파이썬과 다른 C언어의 특성들 (0) | 2025.04.10 |