[WEEK01] 복잡도와 정렬

Krafton Jungle/2. Keywords

[WEEK01] 복잡도와 정렬

munsik22 2025. 3. 16. 17:43

복잡도

알고리즘의 분석

정확한 알고리즘으로 생성되더라도 프로그램을 실행시키기 위해 필요한 시간이나 데이터를 저장하기 위한 공간, 프로그램 변수 등이 너무 커 입력에 대해서 필요가 없을 가능성이 존재함
알고리즘을 실행하는데 필요한 시간과 기억장소의 크기(공간)을 측정하는 일

복잡도의 정의

알고리즘을 실행하는 데 필요한 시간과 공간의 크기
시간 복잡도와 공간 복잡도로 구성됨 (가장 중요한 요인은 시간임)

복잡도의 종류

Best-case time (최선 경우 시간) : n의 크기의 입력을 받는 알고리즘을 실행시키는 데 필요한 최소 시간
Worst-case time (최악 경우 시간) : n의 크기의 입력을 받는 알고리즘을 실행시키는 데 필요한 최대 시간
Average-case time (평균 경우 시간) : n의 크기의 입력을 받는 알고리즘을 실행시키는 데 필요한 평균적인 시간

복잡도의 표기

Big-Oh 표기법 : f(n) = O(g(n)) → g는 f의 점근적 상한선이다.
| f(n) | ≤ C | g(n) |을 만족시키는 양수 C가 존재한다.
빅오 표기법은 알고리즘의 성능을 최악의 경우에 기반하여 분석한다. 이는 알고리즘이 가장 비효율적으로 동작할 때의 성능을 나타내므로, 안정적인 성능 예측을 가능하게 한다.
빅오 표기법에서 상수항과 최고 차항 이외의 항들은 무시된다. (예) 60n² + 5n + 1= O(n²)

시간 복잡도

시간복잡도란 알고리즘이 문제를 해결하는 데 걸리는 시간을 수학적으로 표현한 것이다. 일반적으로 입력의 크기(n)에 따라 소요되는 시간의 증가율을 나타낸다. 시간복잡도를 분석하는 이유는 알고리즘의 효율성을 비교하고, 최적의 알고리즘을 선택하기 위함이다.

O(1) : 입력값(n)에 관계 없이 일정하게 문제 해결에 하나의 단계만을 거침 (예 : 스택의 삽입, 삭제)
O(log₂n) : 문제 해결에 필요한 단계가 입력값(n) 또는 조건에 의해 감소 (예 : 이진 트리, 이진 검색)
O(n) : 문제 해결에 필요한 단계가 입력값(n)과 1:1의 관계를 가짐 (예 : for문)
O(nlog₂n) : 문제 해결에 필요한 단계가 n(log₂n)번만큼 수행 (예 : 힙 정렬, 합병 정렬)
O(n²) : 문제 해결에 필요한 단계가 입력값(n)의 제곱만큼 수행 (예 : 삽입 정렬, 쉘 정렬, 선택 정렬, 버블 정렬, 퀵 정렬)
O(2ⁿ) : 문제 해결에 필요한 단계가 2의 입력값(n) 제곱만큼 수행 (예 : 피보나치 수열)

공간 복잡도

공간복잡도는 알고리즘이 문제를 해결하는 데 필요한 메모리 공간의 양을 나타낸다. 입력의 크기(n)에 따라 메모리 사용량이 어떻게 변하는지를 분석한다.

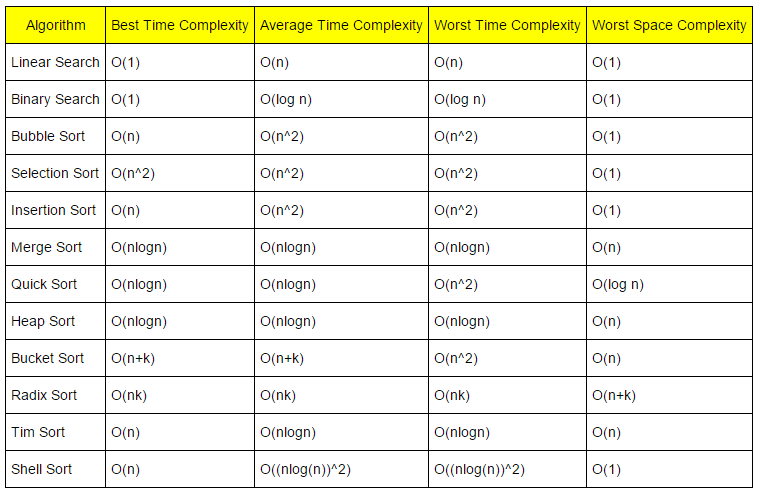
[출처] Sorting And Searching Algorithms - Time Complexities Cheat Sheet ❘ HackerEarth

정렬

버블 정렬 (Bubble Sort) : O(n²)

이웃한 두 원소의 대소 관계를 비교해 필요에 따라 교환을 반복하는 알고리즘 (단순 교환 정렬)
서로 인접한 원소를 비교하여 위치를 변경함, 첫번째부터 마지막-1 번째 원소까지 반복함

1회전 : 85624 : 58624 → 56824 → 56284 → 56248
2회전 : 56248 : 56248 → 52648 → 52468
3회전 : 52468 : 25468 → 24568
4회전 : 24568

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr

선택 정렬 (Selection Sort) : O(n²)

가장 작은 원소부터 선택해 알맞은 위치로 옮기는 작업을 반복하며 정렬하는 알고리즘

첫번째 원소 자리 : 85624 → 25684
두번째 원소 자리 : 25684 → 24685
세번째 원소 자리 : 24685 → 24586
네번째 원소 자리 : 24586 → 24568

def selection_sort(arr):
    n = len(arr)
    for i in range(n):
        min_index = i
        for j in range(i+1, n):
            if arr[j] < arr[min_index]:
                min_index = j
        arr[i], arr[min_index] = arr[min_index], arr[i]
    return arr

삽입 정렬 (Insertion Sort) : O(n²)

주목한 원소보다 더 앞쪽에서 알맞은 위치로 삽입하며 정렬하는 알고리즘
선택 정렬과 비슷하지만, 가장 작은 원소를 선택하지 않는다는 점이 다름
이미 순서화된 파일에 n번째 키를 앞의 n-1개의 키와 비교하여 정렬
두번째 값부터 이전 값들과 비교를 시작함
비교하는 값을 Key라고 할 때, 순서를 변경해야 한다면 Key를 변경 할 자리에 삽입하고 그 자리에 있던 값은 뒤로 한 칸 이동 시킴
정렬된 부분과 정렬되지 않은 부분으로 나누고, 정렬되지 않은 부분의 첫 번째 요소를 정렬된 부분에 알맞은 위치에 삽입하는 방식

key = 5 : 85624 → 58624
key = 6 : 58624 → 56824
key = 2 : 56824 → 25674
key = 4 : 25684 → 24568

def insertion_sort(arr):
    n = len(arr)
    for i in range(1, n):
        key = arr[i]
        j = i - 1
        while j >= 0 and key < arr[j]:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key
    return arr

셸 정렬 : O(n²) ~ O(n log n) ~ O(n)

단순 삽입 정렬의 장점은 살리고 단점은 보완해 더 빠르게 정렬하는 알고리즘
└ 장점 : 이미 정렬을 마쳤거나 정렬이 거의 끝나가는 상태에서는 속도가 아주 빠름
└ 단점 : 삽입할 위치가 멀리 떨어져 있으면 이동 횟수가 많아짐
먼저 정렬할 배열의 원소를 그룹으로 나눠 각 그룹별로 정렬을 수행함
그 후 정렬된 그룹을 합치는 작업을 반복해 원소의 이동 횟수를 줄임

5와 8 비교 : 85624 → 58624
6와 5, 8 비교 : 58624 → 56824
2와 8, 6, 5 비교 56824 → 25684
4와 8, 6, 5 비교 : 25684 → 24568

def shell_sort(arr):
    n = len(arr)
    gap = n // 2

    while gap > 0:
        for i in range(gap, n):
            temp = arr[i]
            j = i
            while j >= gap and arr[j - gap] > temp:
                arr[j] = arr[j - gap]
                j -= gap
            arr[j] = temp
        gap //= 2
    return arr

퀵 정렬 (Quick Sort) :O(n²) ~ O(n log n) ~ O(n log n)

일반적으로 사용되는 가장 빠른 정렬 알고리즘
하나의 그룹을 부분적으로 나누어 가면서 정렬하는 방법
피벗을 기준으로 작은 값을 왼쪽, 큰 값을 오른쪽 서브 그룹으로 분할하는 방식으로 정렬
피벗을 선택한 후, 피벗보다 작은 요소들은 왼쪽, 큰 요소들은 오른쪽으로 이동시키는 방식

초기 배열: [8, 5, 6, 2, 4], 피벗: 6
분할: [5, 2, 4] (왼쪽)와 [8] (오른쪽)
왼쪽 배열 [5, 2, 4]에서 피벗 4 선택 → 분할: [2]와 [5]
최종 병합: [2, 4, 5] → [2, 4, 5, 6, 8]

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)

병합 정렬 (Merge Sort) : O(n log n)

배열을 앞부분과 뒷부분의 두 그룹으로 나누어 각각 정렬한 후 병합하는 작업을 반복하는 알고리즘
분할 정복 알고리즘으로, 리스트를 반으로 나누어 각각 정렬한 후 두 개의 정렬된 리스트를 병합하는 방식

초기 배열: [8, 5, 6, 2, 4]
나누기: [8, 5]와 [6, 2, 4]
[8, 5] 나누기: [8]와 [5] → 병합 후 [5, 8]
[6, 2, 4] 나누기: [6]와 [2, 4]
[2, 4] 나누기: [2]와 [4] → 병합 후 [2, 4]
병합: [6]과 [2, 4] → [2, 4, 6]
최종 병합: [5, 8]과 [2, 4, 6] → [2, 4, 5, 6, 8]

def merge_sort(arr):
    if len(arr) > 1:
        mid = len(arr) // 2
        L = arr[:mid]
        R = arr[mid:]
        merge_sort(L)
        merge_sort(R)
        i = j = k = 0
        while i < len(L) and j < len(R):
            if L[i] < R[j]:
                arr[k] = L[i]
                i += 1
            else:
                arr[k] = R[j]
                j += 1
            k += 1
        while i < len(L):
            arr[k] = L[i]
            i += 1
            k += 1
        while j < len(R):
            arr[k] = R[j]
            j += 1
            k += 1
    return arr

힙 정렬 (Heap Sort) : O(n log n)

힙의 특성을 이용하여 정렬하는 알고리즘
힙 : 부모의 값이 자식의 값보다 항상 크다는 조건을 만족하는 완전 이진 트리
힙 구성 단계: 주어진 배열을 최대 힙으로 변환한다. 최대 힙에서는 부모 노드가 자식 노드보다 항상 크거나 같아야 한다.
정렬 단계: 최대 힙의 루트(최대값)를 배열의 마지막 요소와 교환하고, 남은 요소들로 다시 최대 힙을 구성하는 과정을 반복한다. 이 과정을 통해 배열이 정렬된다.

첫 번째 단계: [4, 5, 6, 2, 8] (8을 마지막으로 이동)
두 번째 단계: [6, 5, 4, 2, 8] (7을 마지막으로 이동)
세 번째 단계: [5, 4, 2, 6, 8]
네 번째 단계: [2, 4, 5, 6, 8]
마지막 단계: [2, 4, 5, 6, 8]

def heapify(arr, n, i):
    largest = i  # 루트
    left = 2 * i + 1  # 왼쪽 자식
    right = 2 * i + 2  # 오른쪽 자식

    # 왼쪽 자식이 루트보다 큰 경우
    if left < n and arr[left] > arr[largest]:
        largest = left

    # 오른쪽 자식이 현재 가장 큰 값보다 큰 경우
    if right < n and arr[right] > arr[largest]:
        largest = right

    # 가장 큰 값이 루트가 아닌 경우
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]  # 교환
        heapify(arr, n, largest)  # 재귀 호출로 힙 구조 유지

def heap_sort(arr):
    n = len(arr)

    # 최대 힙 구성
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)

    # 요소를 하나씩 꺼내어 정렬
    for i in range(n - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]  # 최대값을 배열의 끝으로 이동
        heapify(arr, i, 0)  # 힙 재구성

    return arr

계수 정렬 (Counting Sort) : O(n)

주어진 배열의 값의 범위가 작은 경우 빠른 속도를 갖는 정렬 알고리즘
최댓값과 입력 배열의 원소 값 개수를 누적합으로 구성한 배열로 정렬을 수행함

nums = [4, 2, 2, 8, 3, 3, 1]를 계수 정렬하는 과정을 알아보자.

입력한 배열의 최대값의 길이를 가지는 count 배열 생성
nums의 각 요소가 몇 번 나왔는지 횟수를 기록

1 2 3 4 5 6 7 8

1 2 2 1 0 0 0 1
이전까지의 누적개수를 기록하는 cumCount 배열 생성

1 2 3 4 5 6 7 8

0 1 3 5 6 6 6 6
cumCount 배열에 따라 각 요소의 인덱스 위치를 결정

0 1 2 3 4 5 6

1 2 2 3 3 4 8

def count_sort(arr):
    max_val = max(arr)
    count = [0] * (max_val + 1)

    for i in arr:
        count[i] += 1
    # print(count[1:])

    cum_count = [0] * (max_val + 1)
    for i in range(1, len(count)):
        cum_count[i] = cum_count[i-1] + count[i-1]
    # print(cum_count[1:])

    result = [0] * len(arr)
    for i in arr:
        result[cum_count[i]] = i
        cum_count[i] += 1

    return result

'Krafton Jungle > 2. Keywords' 카테고리의 다른 글

[WEEK02] 이진 탐색 (0)	2025.03.20
[WEEK01] 완전 탐색 (0)	2025.03.18
[WEEK01] 정수론 (0)	2025.03.15
[WEEK01] 반복문과 재귀 함수 (0)	2025.03.15
[WEEK01] 배열과 문자열 (0)	2025.03.15

현재글[WEEK01] 복잡도와 정렬

MUNSIK BLOG

munsik22 님의 블로그 입니다.

합격후기, 정보처리기사, 레드블랙트리, pintos, 백준, csapp, webproxy, 오답노트, 나만무, C, 문식이, 프로그래머스, 크래프톤정글, NextJS, springboot, C++, malloc,

Today :
Yesterday :

일	월	화	수	목	금	토
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30	31

[Munsik] MUNSIK BLOG [Munsik]